
PARAGLIDER DESIGN HANDBOOK
CHAPTER 1. PLATFORM
1.1
Introduction
1.2.
Geometric Definition
1.2.1 Analytical methods
1.2.2 Discrete method
1.3
Center of gravity
1.1. Introduction
The platform in a paralider is one of the most important elements
involved in
the design of it. Any design should begin with the picture of the
platform.
Major elements:
We can distinguish the following basic elements of the platform:
- The leading edge
- The trailing edge
- The tips
Of course, the designs are symmetrical in plan to maintain the same
properties on one side and one wing.
Historically, have experimented with a variety of platforms:
rectangular, trapezoidal, triangular, elliptical, rectangles truncated,
arrow regressive, with Colita morros central or core, ... But now
almost all forms designs tend to look an elliptical with tips
slightly truncated.
The most important parameters of the platforms are as follows:
Parameter
|
unit
|
variable name
|
Area
|
m2
|
area
|
Wingspan
|
m
|
span
|
Max chord
|
m
|
maxch
|
Medium chord
|
m
|
medch
|
Minimum chord
|
m
|
minch
|
Aspect ratio (flat)
|
dimensionless
|
AR
|
Center of gravity
|
m
|
cdg
|
1.2. Geometric
Definition
1.2.1 Analytical
methods
There are many possible methods for defining the plant. On that follows
is one of mathematical methods possible.
In Cartesian coordinates the equation of the ellipse centre (0.0) is:
x ² / a ² + y2 / b ² = 1
For a generic center in (x0, y0) is:
(x-x0) ² + (y-y0) ² = 1
clearing and function is obtained x: y = y0 +-b * sqrt (1 - ((x-x0)
²) / in ²)
Actually, it is not obliged to choose a form exactly elliptical for the
leading edge or the edge of flight, why can change the equation by
adding any other mathematically. To simplify linear add a variation to
the tips such as:
if 0 <x <= kx and 0
if x> and xk = k * (x-xk) (k, xk parameters to choose)
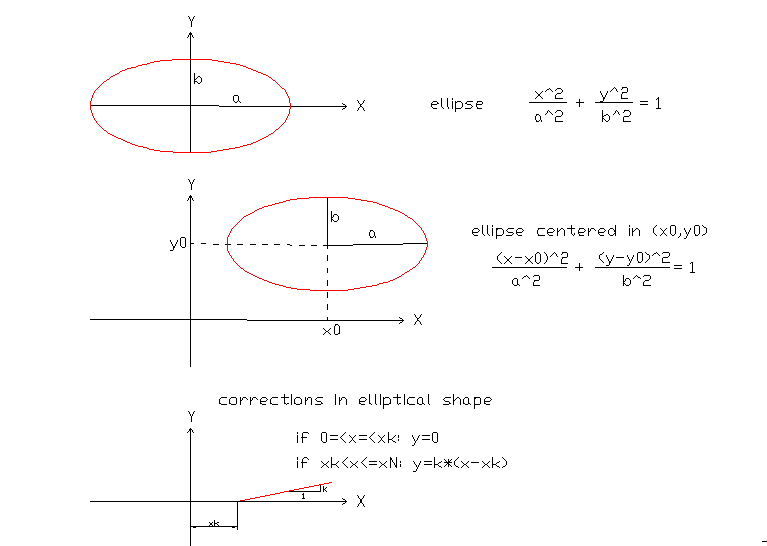
Fig 1. Equation of the ellipse
Taking values x0 = 0 (x-axis centered ellipse), the shape of leading
edge elliptical amended parameters elliptical a1, b1, k1 parameter
linear, and focused on the point (0, y1) is:
Leading edge: y = y1 + b1 * sqrt (1 - (x ²) / a1 ²) + x * k1
Similarly, the shape of elliptical edge output parameters modified
elliptical a2, b2, linear parameters k2, and focused on the point (0,
y2) is:
Trailing edge: y = y2-b2 * sqrt (1 - (x ²) / a2 ²) + x * k2
With these equations and also choosing the correct parameters can be
defined completely the platform of a modern glider.
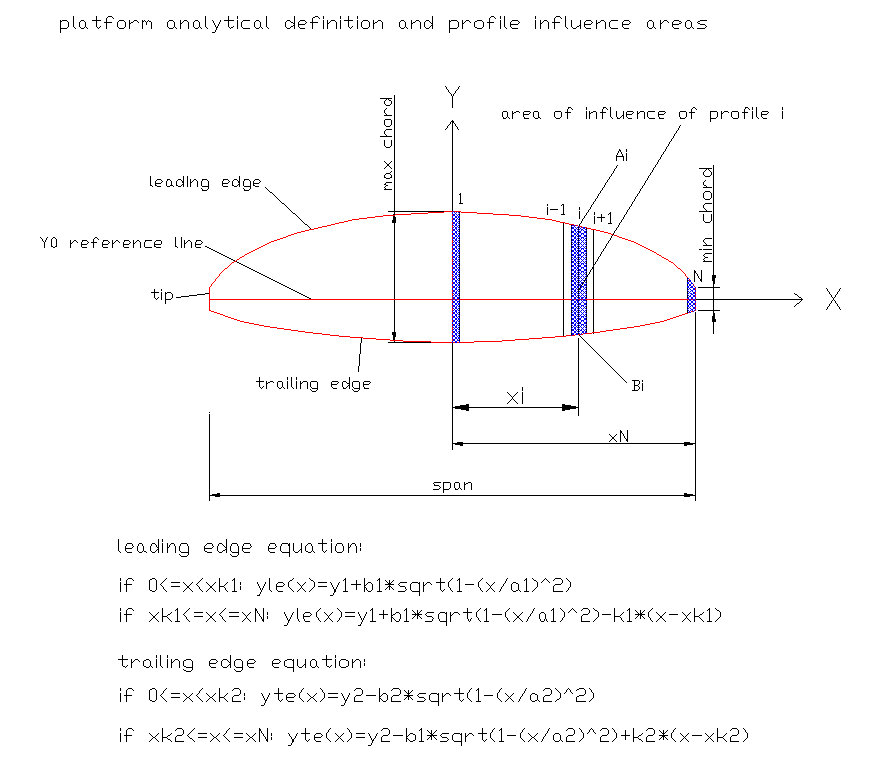
Fig 2. Analytical platform definition
By way of example, shows the values of the parameters of a design: (in redaction)
1.2.2 Discrete
method:
The discreet method is to give directly to each profile,
coordinates
"Y" of the leading edge (Ai) and coordinate "Y" of the trailing edge
(Bi), forming the triplets:
(xi, Ai, Bi) for i = 1,2,3 ,.... N N being the number
of profiles in a semi-wing
The coordinates Ai and Bi can be obtained from equations, of drawings
by hand or with computer, other wings ... and allow maximum freedom to
define the platform.
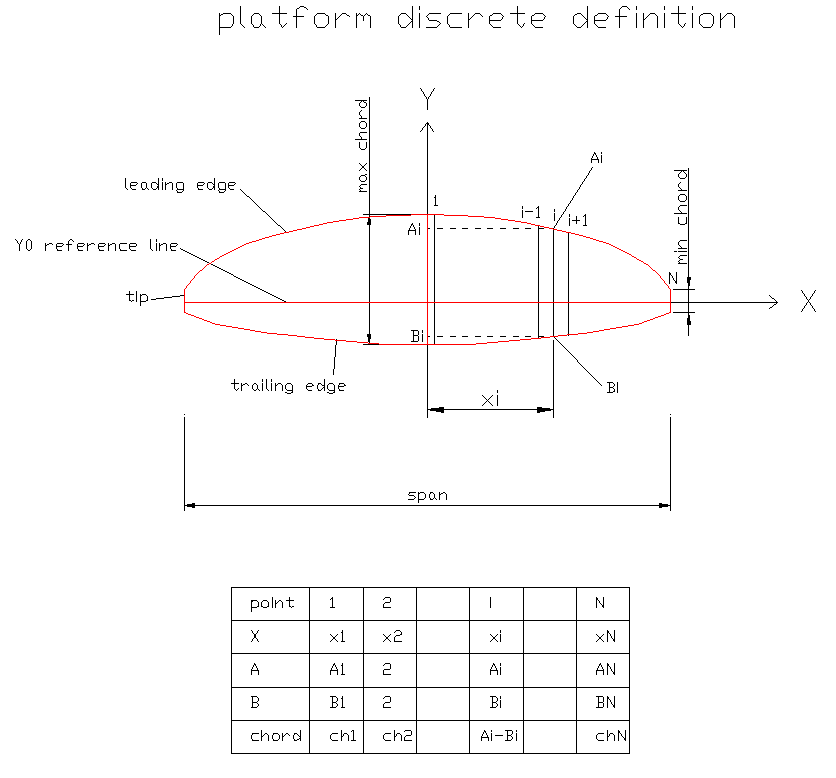
1.3 Center of gravity
The centre of gravity of the
platform, has no direct relationship
aerodynamics, but the knowledge is of interest, since some designers
get very interesting empirical relationships with the position of the
center of pressure.
(...)




