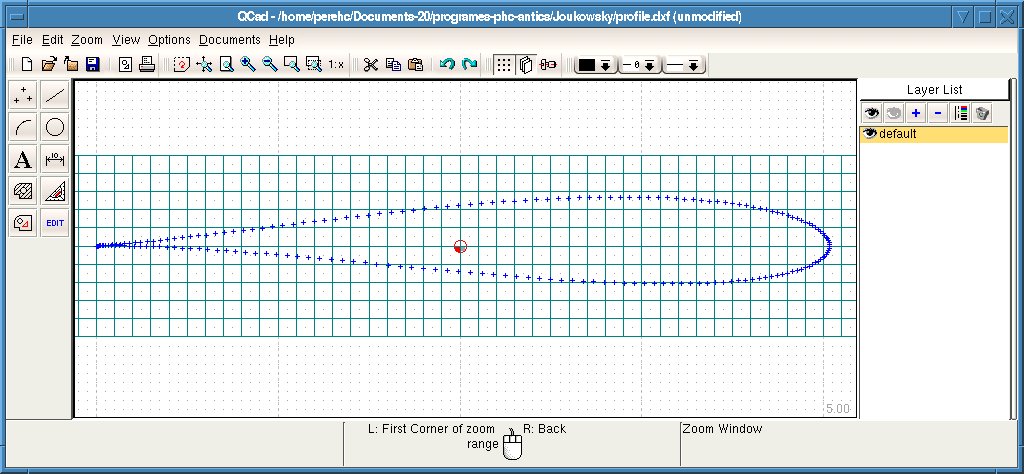
2. Output example file "profile.dxf" viewed in CAD program





3. Source code (FORTRAN 77):


c***************************************************************
c      J O U K O W S K I   A I R F O I L S      v 0.1    
c      Pere Hernández Casellas
c      Laboratori d'envol
c      perehc AT geocities DOT com
c      Version 2005-02-06
c      Adapted to FORTRAN g77 (GNU/Linux)
c      Released under the GNU General Public License 
c      http://www.gnu.org
c***************************************************************


        program joukowsky

        real x1,y1,x2,y2
        real p1x,p1y,p2x,p2y
        real c,a,beta
        integer color
        integer linecolor,pointcolor

c       The program creates "profile.dxf" for viewing whit standard CAD package
c       and "profile.txt" standard text file whit x-y airfoil coordinates

        open(unit=20,file='profile.dxf')
        open(unit=22,file='profile.txt')

        x1=0.
        y1=0.
        x2=100.
        y2=80.
        color=2

        pi=4.*atan(1.)


10      CONTINUE

c       Basic Joukowsky parameters, enter by hand       
        c=100. ! Units cm. Chord reference=4c aprox
        a=110. ! Radius of circunference to transform (a >=c)
        espsil=0.5*((a/c)-1.)
        beta=0.02 ! angle BM-BO

        step=2*pi/200. ! number of points to plot

        write (*,*) "Laboratori d'envol JOUKOWSKY AIRFOILS"
        write (*,*) "Released under GNU General Public License"
        write (*,*)
        write (*,*)

c       Angle M-O-A
        aa=a*sin(beta)
        bb=a*cos(beta)-c
        xm=sqrt(aa*aa+bb*bb)
        delta=atan(aa/bb)

c       Draw ortogonal grid

        color=4 ! use your CAD colors

        ximin=-600.
        ximax=600.
        xjmin=-50.
        xjmax=50.
        xstep=10.

        do xj=xjmin,xjmax,xstep
        call line(ximin,xj,ximax,xj,color)
        end do
        do xi=ximin,ximax,xstep
        call line(xi,xjmin,xi,xjmax,color)
        end do

c       Draw the joukowsky airfoil

        color=9

        do o=0.,2*pi,step

        x=xm*cos(delta)+a*cos(o)
        y=xm*sin(delta)+a*sin(o)
        r=x*x+y*y
        if (r.ne.0.) then
        xi=x*(1.+c*c/r)
        et=y*(1.-c*c/r)

        call point(xi,et,color)

        end if

        end do

c       Compute x-y coordinates

        do o=0.,2*pi,step

        x=xm*cos(delta)+a*cos(o)
        y=xm*sin(delta)+a*sin(o)
        r=x*x+y*y
        if (r.ne.0.) then
        xi=x*(1.+c*c/r)
        et=y*(1.-c*c/r)
        write(*,*) o*180./pi,xi,et
        write(22,*) xi,et
        end if
        end do



1000    continue
        write (*,*) pi,a,c,b
                                                                                                                        


!###########################################################
c     Close the output .dxf file

      write(20,'(/,A,/,I1,/,A)') "ENDSEC",0,"EOF"

c     Close units

      close (20)
      close (22)

      end

!###################################################################

      SUBROUTINE line(p1x,p1y,p2x,p2y,linecolor)
c     line P1-P2
      integer linecolor
      write(20,'(A,/,I1,/,A)') "LINE",8,"default"
      write(20,'(I1,/,A)') 6,"CONTINUOUS"
      write(20,'(I2,/,F6.1,/,I2,/,F6.1)') 10,p1x,20,p1y
      write(20,'(I2,/,F6.1,/,I2,/,F6.1)') 11,p2x,21,p2y
      write(20,'(I2,/,I2,/,I2,/,I2,/,I2)') 39,0,62,linecolor,0
      return
      end

      SUBROUTINE point(p1x,p1y,pointcolor)
c     punt P1
      integer pointcolor
      write(20,'(A,/,I1,/,A)') "POINT",8,"default"
      write(20,'(I1,/,A)') 6,"CONTINUOUS"
      write(20,'(I2,/,F6.1,/,I2,/,F6.1)') 10,p1x,20,p1y
      write(20,'(I2,/,I2,/,I2,/,I2,/,I2)') 39,0,62,pointcolor,0
      return
      end

!##############################################################3